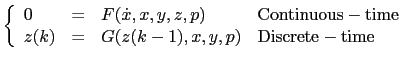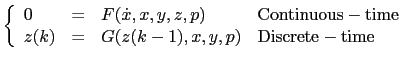Modelica
fr - eng


iGUI - Scicos initialization GUI

Module

Introduction

In this use manual we will focus on initializing Modelica models in Scicos. A Modelica model in general can be expressed as hybrid model. The continuous-time part can be defined with a DAE and the discrete-time part with discrete-time equations, as follows:

$\displaystyle \left\{ \begin{array}{llll} 0&=& F(\dot x,x,y,z,p)& {\rm Continuous-time}\\ z(k)&=&G(z(k-1),x,y,p) & {\rm Discrete-time} \end{array} \right. $

where x, dot(x), y, z, and p are the vector of differential variables, derivative of differential variables, algebraic variables, discrete-time states, and model parameters, respectively [3,4]. A model can be simulated only if it is initialized correctly. A reason lies in the fact that a DAE (Differential-Algebraic Equation) resulting from a Modelica program can be simulated only if the initial value of all variables as well as their derivatives are known and consistent. Furthermore, sometimes the user needs to start the model at a specified initial states, e.g., at equilibrium point.

By default, Scicos supposes that the parameters and the initial value of differential variables (variables whose derivative exist in the Modelica program) are known and given by start keyword (otherwise they are set to zero), then a solver is used to compute the derivative of differential variables and algebraic variables. The user can also give start values of algebraic variables in the Modelica program which are used as guess values to help the solver to find consistent initial values. In many practical applications, this approach of initialization does not cover all forms of initializations. For example, often it is required to start a simulation in the steady state. In this case, derivatives of differential variables are set to zero and the initial values of all the variables are found as a function of known outputs (or observable states). The initialization problem can also be formulated as an inverse problem where the system outputs are known at initial time, and the inputs and internal states are to be computed. Sizing is another form of initialisation, where, e.g., a parameter of the model is computed at steady states as a function of a system output (or observable states).

In ScicosLab, an initialization GUI has been developed providing support for a more general form of initialization. In this initialization GUI, the user can select freely the known and unknowns of the initialization problem between the all Modelica variables, the derivatives of differential variables, discrete-variables, and the parameters of the model. A weight is associated to each value specifying the degree of confidence in that value. The weight varies from zero to one where zero means the value is just a pure guess and one means the guess value corresponds to the actual value. This latter situation corresponds in particular to the usage of the "fixed" keyword in Modelica. With this initialization methodology, no matter if an unknown is a parameter or a differential or algebraic variable, it can be computed as a function of other known values.

Another problem with the previous approach of initialization concerns with start values of algebraic variables. The Modelica compiler of Scicos performs formal simplifications on Modelica programs and generates a DAE which is used for both model initialization and dynamic simulation. Using the simplified Modelica model causes a problem in initialization of big Modelica programs where guess values of algebraic variables are important for convergence of the solver. The generated DAE contains all differential variables and their derivatives, but many algebraic variables are eliminated during the formal simplification phase of the Modelica model. This has several consequences: First, algebraic variables to be eliminated may change when the Modelica model changes a bit. Thus, the user is unable to know in advance what algebraic variables will be selected to provide their guess values. Furthermore, in many cases the remained algebraic variables may not have physical interpretation and the user cannot provide the guess value without performing a calculation.

Because of these difficulties, we decided to separate the model initialization and the dynamic simulation and generate two models for each one. With this approach, the problem of the selection of algebraic variables no longer exists. In fact, once the initialization phase finished, initial values of all algebraic variables as well those of derivatives of differential variables are known. As a consequence, the selection of algebraic variables in the simplified Modelica code does not affect the dynamic simulation.

In Modelica, the start keyword can be used to set start values of variables. Start value of derivatives of variables can be given within initial equation section. For small programs, this method can be easily used but as the program size grows, it becomes difficult to set start values and change the fixed attribute of variables/parameters directly in the Modelica program; initialization via modifying the Modelica model is specially difficult for models with multiple level of inheritance. Then, the user often needs to have a single model but with several initialization scenarios. So, for each scenario a copy of the model should be saved.

Having confronted these inconveniences, we found it easier and more intuitive if start values and other attributes of variables/parameters are provided via a GUI. In the GUI, the user can easily change attributes such as start, max, min, nominal for variables/parameter of a model. Furthermore, it is possible to indicate whether a variable, the derivative of a variable or a parameter must be fixed or relaxed during initialization. It is also possible to save the resulting configuration in a file and use it later.

In the following sections the initialization methodology for Modelica models, the initialization GUI, and available initialization computing methods for continuous-time Modelica models (index-1 DAE) will be explained.

Initialization methodology in Scicos

The first objective of the initialization is to compute consistent initial values for all variables and derivatives of differential variables (for index-1 DAEs). In order to initialize the model, it is first flattened. Then if the model contains derivatives, they should be converted into a pure algebraic model. For that, all derivatives should be replaced by algebraic variables.

\resizebox{!}{130mm}{\includegraphics{flowchart.eps}}
Figure 1 : Initialization in Scicos

The procedure of initialization is given in Figure 1. The initialization is composed of:

In the initialization process, three external applications are used: Translator, XML2Modelica, and modelicac (all developed at LMS Imagine.Lab).

Translator is used for three purposes:

Once the XML file generated, the user can change variable/parameter attributes. The modified XML file should be reconverted into a Modelica program to be compiled and initialized. XML2Modelica is used to perform this task.

Modelicac, which is a compiler for the subset of the Modelica language, compiles a flat Modelica model and generates a C program for Scicos targets. The main features of the compiler are the simplification of the Modelica models and the generation of the C program ready for simulation. It supports discontinuous model switching and provides the analytical Jacobian of the model. It does not support higher index DAEs.

When the user requests a Modelica initialization in Scicos, as shown in Figure 1, Translator is called and first a flat Modelica model, then an XML file are generated. The XML file can then be used in the initialization GUI. The user can change the variable/parameter attributes in the XML file. The modified XML file is then translated back to a Modelica program. The Modelica program is compiled with modelicac and a C program is generated. The C program is used by Scicos to compute the initial value of variables/parameters. Once the initialization finished, whether succeeded or failed, the XML file is updated with the most recent results which the user can visualize and decide if the dynamic simulation should start or not.

At the beginning of the dynamic simulation, the initial values of the variables are read from the XML file and the simulation can start. The results of the dynamic simulation can also be saved in an another XML file to be used as a starting point for another simulation.

Initialization GUI

In order to manipulate an XML file, a GUI has been developed for Scicos. This API has been developed in TCL/TK. A screenshot of this GUI is shown in Figure 1.4.

\begin{figure}\begin{center} \epsfig{file=IHM2.eps,width=500pt} \end{center} \end{figure}
Figure 1.4 : Screenshot of the initialization GUI in Scicos

With this GUI, the user can Open/Close/Save XML files and visualize the attributes of variables/parameters. Each variable/parameter has several attributes: name, id, type, fixed, value, weight, max, min, nominal, comment, and selection.

Once the user changes the new attributes of variables/parameters, the initialization process can be invoked by clicking on the compute button. The obtained results, either successful or failed, are put back into the XML file and new values are displayed. If failed, the user can select another computing methods available and iterate until a consistent result is obtained.

Computation methods

The initialization problem is generally defined as the solution of a nonlinear system of equations

$\displaystyle 0=F(X)$

where X is a vector composed of all the variables, derivatives of the differential variables (transformed into algebraic variables), and relaxed parameters (fixed=false). The initialization GUI provides several computation methods for initialization. None are guaranteed to converge, so the user should try sequentially several available methods until one works. This is possible because, if one method fails, another method can be tried using the last obtained result. In this section these methods as well as their characteristics will presented.

KINSOL

SUNDIALS [5,6] is a family of solvers which includes CVODE, for systems of ordinary differential equations, CVODES, systems of nonlinear algebraic equations, and IDA, for systems of differential-algebraic equations.

CVODE and IDA solvers have already been integrated in Scicos for dynamic simulation of models. KINSOL includes an optional user-callable module to recompute the initial conditions so as to be consistent with the given DAE system. This module uses inexact Newton methods with line-search strategies for accelerated convergence. This solver provides the possibility of scaling variables, provided via Nominal value of the variable. The user can select if this method uses an analytical Jacobian or not. An analytical Jacobian provides better convergence.

IDA

IDA includes an optional user-callable module to recompute the initial conditions so as to be consistent with the given DAE system. This module uses inexact Newton methods with line-search strategies for accelerated convergence. We used this feature of IDA for initialization of models. IDA also permits inequality constraints to be imposed on the solution components. This can be used to implement max/min attributes used in Modelica.

The user can select if this method uses an analytical Jacobian or not. An analytical Jacobian provides better convergence.

Fsolve

Similar to IDA, Fsolve finds a zero of a system of nonlinear functions. This solver is based on the Modified Newton method and uses the QR factorization technique. This solver often obtains less precise but more robust solutions than previous solvers.

Optim

When the Modelica model is flattened, several variables exist for which start values are not given by the user. The compiler sets their start values to zero. It happens very often that the Jacobian matrix associated with the nonlinear equations in the very first step becomes singular, e.g., consider the equation set (1) with $ X(0)=[0,0]^t$ start values.

\begin{equation} F(X):\left\{ \begin{array}{lll} 0&=&x-1\\ 0&=&xy-1\\ \end{array}\right. \end{equation}

The first computed Jacobian matrix is singular and the Newton method fails. In order to overcome this problem, the user can choose the Optim solver. In this case, Scicos tried to obtain the solution by minimizing the cost function C(X).

\begin{equation} C(X)=\sum^{N}_{i=1}f_i^2(X) \end{equation}

The result of this optimization provides non-zero values that may be used as new start values for other methods, such as Sundials.

Model Tree

In the left hand side of the iGUI the model is displayed as a hierarchical tree. Each main branch designates an instance of a block. The name of a branch is composed of tree parts: the base-name of the block, the identification of the block which is defined in Scicos windows (right clicking on the block a pop-up menu appears, then clicking on the Identification item), and a number if there are two blocks with the same name and the same identification.

Double clicking on each branch (block), the corresponding block in Scicos will be highlighted.

Clicking on the cross of each branch, the variables and parameters defined in that block will be displayed at right hand side of the GUI. A block may have sub-components, connectors, vector/matrix variables, etc. In this case, these items are displayed with sub-branches, See Figure 2.

Pull-down Menus

File

Derivative

A dynamic model consists of variables and their derivatives. In initialization of these models, the user should decide what to do about the derivative of differential variables. There are two options:

Of course after selecting one of these option, the user can also manually change if a variable is fixed or not.

When the iGUI is launched, if the model contains any derivatives, the user is asked to select one of there options or do it later.

Display

Being in any mode, double-clicking on the hierarchical tree in the left sub-frame, the display mode is set to "Normal".

Code generation

Search Button

With this edit field, the user can search for a variable or a parameter. The ID of all variables are compared with the searched text, if compatible, the variable is displayed.

Note than the search is case-sensitive. In order to return back to normal display mode, you can either select "Normal" from Display menu, or double click on the tree at the left hand side of the iGUI.

Information bar

Solve Button

Clicking on this button, the model is compiled and a C code is generated. Before compiling is is verified if number of unknowns agrees with number of equations. If they are not equal, a message warns the user. The button remains disable until the solver ends the work. Either successful or not, the new obtained results are displayed in the iGUI, and the Solve button is enabled. and the user can try again either using the same solver, another solver, or using a code with analytical Jacobian.

Error

In this box the infinite norm of the residual of the solution (maximum error value) is displayed. When the error value is unknown (at the beginning) or when it becomes NaN or INF, a "?" sign is displayed.

Example

Consider the electrical circuit shown in Figure 1.10. This circuit has been modeled with Modelica blocks in Scicos. The initialization GUI for this circuit is shown in Figure 1.4. For this electrical circuit, we would like to use the initialization GUI for two purposes: initialization from equilibrium state and for parameter sizing.

\begin{figure}\begin{center} \epsfig{file=RLC.eps,width=350pt} \end{center} \end{figure}
Figure 1.10 : An electrical circuit to be initialized

It is interesting to note that several initializations can be performed without modifying the Modelica program. Each initialization can be saved in an XML file and be used later.

XML file example

RLC_circuit_imf_init.xml 

<model>
<name>RLC_circuit_imf</name>
  <elements>
<struct>
<name>Capacitor_</name> 
<subnodes>
<terminal>
<name>__der_v</name>
<kind>variable</kind>
<id>Capacitor_.__der_v</id>
<fixed value="false"/>
<initial_value value="0."/>
<nominal_value value=""/>
<comment value="Time derivative of Capacitor_.v"/>
<selected value="y" />
</terminal>
<terminal>
.....
<terminal>
<name>vi</name>
<kind>variable</kind>
<id>OutPutPort_1.vi</id>
<fixed value="false"/>
<initial_value value=""/>
<nominal_value value=""/>
<comment value=""/>
</terminal>
</subnodes>
</struct>
  </elements>
<equations>
<equation value="	`Inductor_.i` = `Inductor_.p.i`;"/>
<equation value="	`Inductor_.n.i` = (- `Inductor_.i`);"/>
<equation value="	`Inductor_.v` = (`Inductor_.p.v` - `Inductor_.n.v`);"/>
<equation value="	(0.0001 * `Inductor_.__der_i`) = `Inductor_.v`;"/>
<equation value="	`Capacitor_.i` = `Capacitor_.p.i`;"/>
<equation value="	`Capacitor_.n.i` = (- `Capacitor_.i`);"/>
<equation value="	`Capacitor_.v` = (`Capacitor_.p.v` - `Capacitor_.n.v`);"/>
....
<equation value="	`VsourceAC_.p.v` = `Ground_.p.v`;"/>
<equation value="	`CurrentSensor_.p.v` = `Ground_.p.v`;"/>
<equation value="	`Resistor_.p.v` = `VsourceAC_.n.v`;"/>
<equation value="	`VoltageSensor_.v` = `OutPutPort_.vi`;"/>
<equation value="	`CurrentSensor_.i` = `OutPutPort_1.vi`;"/>
</equations>
  <when_clauses>
  </when_clauses>
</model>

Bibliography

1
S. L. Campbell, J.P. Chancelier, R. Nikoukhah, Modeling and simulation in Scilab/Scicos, Springer Verlag publishing, 2005.

2
J. P. Chancelier, F. Delebecque, C. Gomez, M. Goursat, R. Nikoukhah, S. Steer, An introduction to Scilab, Springer Verlag, Le Chesnay, France, 2002.

3
K. E. Brenan, S. L. Campbell, and L. R. Petzold, Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations, SIAM publication, Philadelphia, 1996.

4
P. N. Brown, A. C. Hindmarsh, and L. R. Petzold, "Consistent initial condition calculation for differential-algebraic systems", SIAM J. Sci. Comp., no. 19, 1998.

5
A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker, and C. S. Woodward, "SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers," ACM Transactions on Mathematical Software, 31(3), pp. 363-396, 2005.

6
A. C. Hindmarsh, "The PVODE and IDA Algorithms," LLNL technical report UCRL-ID-141558, December 2000.

7
E.L. Allgower and K. Georg, Numerical Continuation Methods, an Introduction, Springer Ser. in Comput. Math. Springer-Verlag, Vol 13, 1990.

8
E.L. Allgower and K.Georg, "Continuation and path following", Acta Numerica, 1993, pp. 1-64.

9
Kenneth S. Kundert. ``The designer's guide to Spice and Spectre''. Kluwer academic publishers, 1995.

10
A. Dyess, E. Chan, H. Hofmann, W. Horia, and Lj. Trajkovic, "Simple implementations of homotopy algorithms for finding dc solutions of nonlinear circuits", Proc. IEEE Int. Symp. Circuits and Systems, Orlando, FL, Vol. VI, 1999, pp. 290-293.

11
W. Mathis, Lj. Trajkovic, M. Koch, and U. Feldmann, "Parameter embedding methods for finding dc operating points of transistor circuits", Proc. NDES '95, Dublin, Ireland, 1995, pp. 147-150.

12
L.T. Watson, Appl. Math. Comput. 5 (1979), pp. 297-311.

13
L.T. Watson, "Golobally convergent homotopy algorithm for nonlinear systems of equations", Nonlinear Dynamics, Vol. 1, 1990, pp. 143-191.

14
L. T. Watson, M. Sosonkina, R. C. Melville, A. P. Morgan, and H. F. Walker, "Algorithm 777: HOMPACK90: A suite of FORTRAN 90 codes for globally convergent homotopy algorithms", ACM Trans. Math. Software, Vol. 23, 1997, pp. 514-549.

15
B. C. Eaves, "A Short Course in Solving Equations with PL Homotopies", SIAM-AMS Proceedings IX, 1976, pp. 73-143.

16
K. Georg," An introduction to PL algorithms: Computational solution of nonlinear systems of equations", Lectures in Applied Mathematics, American Mathematical Society, 26, 1990, pp. 207-236.

17
W.P.M.H. Heemels, J.M. Schumacher, and S. Weiland, "Linear complementarity systems", SIAM Journal on Applied Mathematics,Vol. 60 (2000), pp. 1234-1269.

18
C.E. Lemke, and J.T. Howson, "Equilibrium points of bimatrix games", SIAM J. Appl. Math., Vol. 12, 1964, pp. 413-423.

19
D. M.W. Leenaerts, W.M.G. van Bokhoven. Piecewise Linear Modelling and Analysis. Kluwer Academic Publishers, Boston, 1998.

Authors

Masoud Najafi INRIA