LOOKUP

Scicos Block
fr - eng

1D Lookup table

$\epsfig{file=LOOKUP_c.eps,height=90pt}$

1D Lookup table

Lookup Table block realizes a non-linear function defined using a graphical editor. This block computes an approximation to some function y=f(x) given data vectors x and y.
The table is defined by specifying the Vector of input values parameter as a 1-by-n vector and the Table data parameter as a 1-by-n vector. The block generates output based on the input values using one of methods selected from the Lookup method parameter list. The length of the x and y data vectors provided to this block must be identical. Furthermore, the x data vector must be strictly monotonically increasing.

Dialog box

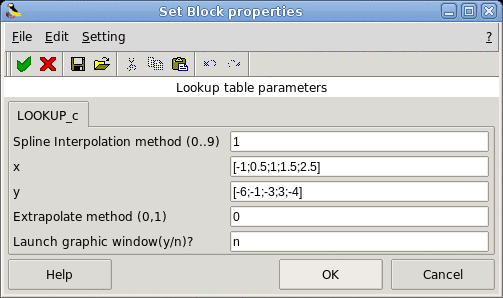
$\begin{figure}\begin{center} \epsfig{file=LOOKUP_c_gui.eps,width=300pt} \end{center}\end{figure}$

Spline Interpolation method (0..9) : accepted values are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
This parameter defines the spline method for interpolating the points. The Signal builder block computes a linear or a cubic spline or sub-spline S which interpolates the (x_i,y_i) points, i.e., we have :

$\displaystyle S(x_i) = y_i\;\; {\rm for\;\; all}\;\; i=1,..,n.$
Several kind of splines may be computed by selecting the appropriate spline method:
- 0 : "Zero order method (Use Input Below)". This method does not interpolate or extrapolate. Instead, the element in x nearest and below the current input is found, i.e.,
  
  $\displaystyle {\rm for} \;\; t_{i} \leq t < t_{i+1},\;\; y(t)=y_{i}.$
  The corresponding element in y is then used as the output. If there is no element in x below the current input, then the nearest element is found.
- 1 : "Linear interpolation method". This is the default method; it performs linear interpolation of the inputs. If a value matches the block's input, the output is the corresponding element in the output vector. If no value matches the block's input, then the block performs linear interpolation between the two appropriate elements of the table to determine an output value, i.e.,
  
  $\displaystyle {\rm for}\;\; t_{i} \leq t < t_{i+1}, \;\; y(t)=y_i+(t-t_i)(y_{i+1}-y_i)/(t_{i+1}-t_i).$
  If the block input is less than the first or greater than the last input vector element, then the block extrapolates using the first two or last two points.
- 2 : "Order 2 method". The interpolation is done by passing 2-order polynomials between (x_i,y_i) and (x_i+1, y_i+1). The Derivative at (x_i,y_i) is identical for two adjacent polynomials. The derivative at (x_1,y_1) can be selected arbitrary, so it is selected such that the sum of derivatives at all points be minimum. This condition provides a less fluctuated signal.
- 3 : "not_a_knot". The cubic spline is computed by using the following conditions (considering n points x_1,...,x_n) :
  
  $\displaystyle S^{(3)}(x_2^-) = S^{(3)}(x_2^+),$
  
  $\displaystyle S^{(3)}(x_{n-1}^-) = S^{(3)}(x_{n-1}^+).$
- 4 : "periodic". A periodic cubic spline is computed (y must verify y_1=y_n) by using the conditions :
  
  $\displaystyle S^{'}(x_1) = S^{'}(x_n),$
  
  $\displaystyle S^{''}(x_1) = S^{''}(x_n).$
  In this case the value of y_n is ignored and y_1 is used instead. Note that in order to generate a periodic signal, Periodic flag should be activated.
- 5 : "monotone". In this case a sub-spline (S is only one continuously differentiable) is computed such that S is monotone on each interval :
  
  $\displaystyle {\rm if}\;\; y_i \le y_{i+1},\;\; S\;\; {\rm is\;\; increasing\;\; on}\;\; [x_i, x_{i+1}].$
  
  $\displaystyle {\rm if}\;\; y_i > y_{i+1},\;\; S\;\; {\rm is\;\; decreasing\;\; on}\;\; [x_i, x_{i+1}].$
- 6 : "clamped". In this case the cubic spline is computed by using the end points derivatives which are set to zero, i.e.,
  
  $\displaystyle S^{'}(x_1) = S^{'}(x_n)=0.$
- 7 : "fast". In this case a sub-spline is computed by using a simple local scheme for the derivative at x_i of the interpolation polynomial of (x_i-1,y_i-1), (x_i,y_i), (x_i+1,y_i+1), except for the end points (derivative at these points are computed from the 3 left most points and the 3 right most points).
- 8 : "Zero order method (Use Input-above)". This method does not interpolate or extrapolate. Instead, the element in x nearest and above the current input is found, i.e.,
  
  $\displaystyle {\rm for}\;\; t_{i} \leq t < t_{i+1},\;\; y(t)=y_{i+1}.$
  The corresponding element in y is then used as the output. If there is no element in x above the current input, then the nearest element is found.
- 9 : "Zero order method (Use Input-nearest)". This method does not interpolate or extrapolate. Instead, the element in x nearest the current input is found. The corresponding element in y is then used as the output.
x : Abscisse data vector (X-axis). This vector can be either a row or a column vector of double data. Further mor it should be monotonic increasing. This vector can be also defined in the Scicos context. The data vector can be specified by mathematical formula.
y : Ordinate data vector (Y-axis). This vector can be either a row or a column vector of double data. Not that the size of X and Y vector should be the same. This vector can be also defined in the Scicos context. The data vector can also be specified by formula.
Extrapolate method (0,1) : If the block input is less than the first or greater than the last input vector element, then
- : 0 the block uses the first or last point as output.
- : 1 the block extrapolates using the first two or last two points.
Launch graphic window(y/n)? : If y is selected, by clicking on OK button, a graphical window is launched. In this 2D graphical window, the user can edit data points.